


WHICH THUS INCLUDES:
01. DDG (Which Is Drop-Dead Gorgeous, If You Don't Know)
02. At the Lab We Work and Play
03. The Age of Mechanical Reproduction
04. Exploder One
05. The Futility of Society
06. One Never Says 'Verbal' When One Means 'Oral'
07. Home with the Device
08. That rascal Freneau
09. Everything
10. Video Game Soundtrack
11. Fair Enough
12. Spanish Plankton
These songs feature the vocal talents of JEN GWIAZDOWSKI
With additional production and guitar by JIM LEE
"Maze" and "Robot" illustrations by ESTHER LUC
Marker portrait and comic by DAVE MERSON-HESS
Various assistance from JAMES CHAN and BEN WRIGHT (thanks)
Track 05 - SO SO MODERN, "At/One/Fell/Swoop"
Track 08 - THE JACKSON 5, "Ain't No Sunshine"; DÄLEK, "Distorted Prose"
Track 11 - SPARKLEHORSE, "Getting It Wrong"
Track 12 - MILES DAVIS, "Spanish Key"
WORKS COVERED OR SAMPLED IN THIS ALBUM ARE SO APPROPRIATED WITHOUT EXPLICIT PERMISSION FROM THE ORIGINAL COPYRIGHT HOLDERS (EXCEPT MAYBE FOR SO SO MODERN, WHO HOPEFULLY DO NOT MIND).
This recording is distributed under the Creative Commons Attribution-NonCommercial 3.0 Unported License.
This is the News was composed and produced in February 2008.


OH YEAH.
"I have heard worse."
"Astonishingly music-like."
"Yet again Gwiazdowski wastes her talents alongside a vastly inferior supporting cast."
"['Fair Enough'] sounds like a Sarah McLachlan cover of an R. Kelley groove."
MAYBE ONE OR TWO THINGS THAT DIDN'T MAKE IT ONTO THE RECORD (INSOFAR AS WE CAN REFER TO IT AS A "RECORD") AND ARE IN PRETTY ROUGH SHAPE, SO DON'T SAY WE DIDN'T WARN YOU:
- "No Sense in Being the Early Bird"
- Which ended up sounding way too organic for the rest of album. It probably reminds you of Iron & Wine.
- Etc. etc. etc.
- Which are yet to be prepared for safe listening.

Now you can impress your friends with a Good Old Neon-prepared mixtape, composed of songs that inspired This is the News. You will soon discover that we are not quite the revolutionary creative minds that we had pretended to be...rather we are reptile-brained hacks! It thereon becomes manifestly clear that our efforts have amounted to no more than the sapless, mocking reconstitution of the work of past greats. Such a meek and flaccid discharge from a pair of third-rate charlatans whose imitations bear out only the cheapest kind of flattery. Of the sort to be flicked away like the off-colored lint on one's cuff. Surely there must be laws against this. What a disgrace.


You will recall the following propositions:
- The sum of the internal angles of a triangle is π radians. (1)
- A line is an angle of π radians. (2)
- A rectangle is a quadrilateral whose internal angles are each π/2 radians. (3)
- A rectangle's area is equivalent to the product of its length and width. (4)
We would do well to make use of the following lemma, the proof of which has been left to the reader as an exercise:
- The area of a triangle is equivalent to one-half of the product of its base length and height. (5)
Now consider the following diagram:
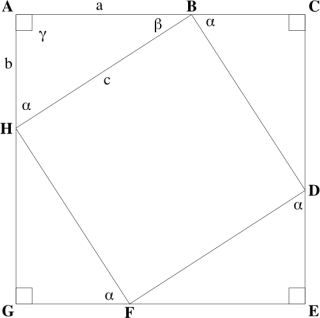
⊿HAB is a right triangle with base length a, height b, and an internal angle between the base and height, γ, of π/2 radians. Our goal is to calculate the length of the hypotenuse, c, in terms of a and b.
Let us propose that the triangles ⊿BCD, ⊿DEF, and ⊿FGH are identical to ⊿HAB. These four triangles are thus arranged to form the quadrilateral ACEG.
At a glance, we may immediately confirm the following:
- By 1 and 2, ∠HBD is congruent to ∠HAB, or equivalent to γ, which is π/2 radians. (6)
- By similar logic, ∠FHB, ∠DFH, and ∠BDF are congruent to ∠HBD. (7)
- By 3, observe that quadrilateral ACEG is a rectangle. (8)
- From 3 and 7, we see that quadrilateral BDFH is also a rectangle. (9)
According to 4, the area of rectangle ACEG is given by
(10) (a + b)²
We can also construct a formula for the area of ACEG using the term c through a composition of the areas of its constituent parts, which include
- the areas of the four triangles ⊿HAB, ⊿BCD, ⊿DEF, and ⊿FGH, which are each ½ab, by 5. (11)
- the area of the central quadrilateral BDFH is c², by 4 and 9. (12)
Therefore, the alternative expression for the area of ACEG is
4(½ab) + c²
which simplilfies to
(13) 2ab + c²
Propositions 10 and 13 thus provide us with two formulae for the area of rectangle ACEG, which produces the following algebraic equivalence:
(a + b)² = 2ab + c²
which, in turn, is easily expanded to
a² + 2ab + b² = 2ab + c²
A further trivial simplification yields substantial fruit, viz., the following elementary expression:
(14) a² + b² = c²
This concludes our proof. Recall how hard Good Old Neon rocks your shit.∎